Seminar for computer science master students (IN2107) and mathematics bachelor and master students.

• Prof. Dr. Daniel Cremers
• Dr. Emanuele Rodolà
• Matthias Vestner
• Thomas Windheuser

The preliminary meeting is over. All topics are already assigned.

Any participant that missed the first meeting should look at the Slides of the preparation meeting. If you still have questions, please do not hesitate to ask by email to Thomas Windheuser .

For all formalities, see our presentation: Slides of the preparation meeting.

Final reports should be written in LaTeX using the provided template: Report template.

* The new report template is now available: Report template

Meetings will always take place on Wednesday 14:00 in room 02.09.023.

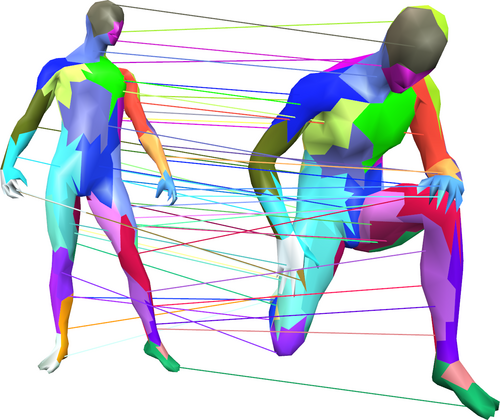
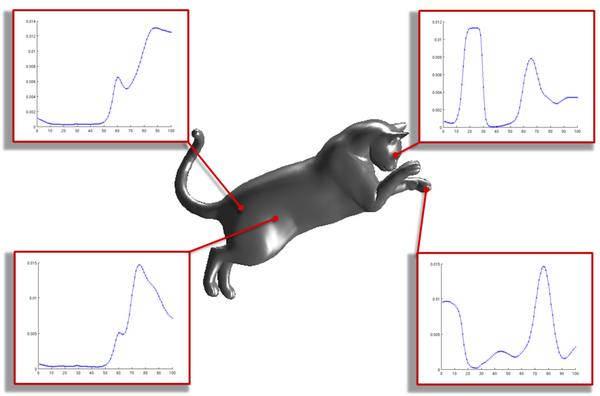
Three-dimensional objects have been used for decades in computer science. Nevertheless, methods for the automatic analysis, recognition, categorization and comparison of these objects have become an active field of research only recently. In this seminar, we will start by reviewing the classical approaches in the literature and then proceed to investigate methods for automatic retrieval and analysis of 3D models. The course will touch upon the most recent advances in the field. Particular emphasis will be put on defining and computing similarity between shapes, when these shapes are allowed to undergo non-rigid deformations (e.g. different poses of a human model). This, in turn, will enable us to discuss further directions of research in real-world scenarios, such as those arising in practical applications where the 3D data is captured with depth sensors (such as the Kinect).

• 13 meetings every Wednesday at 14:00 starting from April 16th
• about 13 participants

• Canzani, Yaiza
  Analysis on manifolds via the Laplacian
• Meyer, M., Desbrun, M., Schröder, P., & Barr, A. H. (2002)
  Discrete differential-geometry operators for triangulated 2-manifolds. Visualization and mathematics, 3(2), 52-58
• R. Rustamov, Laplace-Beltrami Eigenfunctions for Deformation Invariant Shape Representation. In Symposium on Geometry Processing, 2007.
• J. Sun, M. Ovsjanikov, L. Guibas, A Concise and Provably Informative Multi-Scale Signature Based on Heat Diffusion. In Symposium on Geometry Processing , 2009.
• M. Aubry, U. Schlickewei, D. Cremers, The Wave Kernel Signature: A Quantum Mechanical Approach To Shape Analysis. In International Conference on Computer Vision (ICCV) - Workshop on Dynamic Shape Capture and Analysis (4DMOD), 2011.
• M. Ovsjanikov, Q. Huang, L. Guibas Condition Number for Non-Rigid Shape Matching. In Symposium on Geometry Processing, 2011.
• M. Ovsjanikov, M. Ben-Chen, J. Solomon, A. Butscher, L. Guibas, Functional Maps: A Flexible Representation of Maps Between Shapes. In SIGGRAPH, 2012.
• N. Litke, M. Droske, M. Rumpf, and P. Schröder, An image processing approach to surface matching. In Symposium on Geometry Processing, 2005.
• T. Sebastian, P. Klein, B. Kimia, On Aligning Curves. PAMI, 2003.
• F. Mémoli, G. Sapiro, A theoretical and computational framework for isometry invariant recognition of point cloud data. In Found. Comput. Math., 2005.
• A. Bronstein, M. Bronstein, R. Kimmel, Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching, PNAS, 2006.
• S.Kurtek, E. Klassen, Z. Ding, A. Srivastava, A novel Riemannian framework for shape analysis of 3D objects. In CVPR, 2010.
• I. Jermyn, S. Kurtek, E. Klassen, A. Srivastava, Elastic shape matching of parameterized surfaces using square root normal fields. In ECCV, 2012.
• G. Kim, Y. Lipman, T. Funkhouser, Blended Intrinsic Maps. In SIGGRAPH, 2011.
• B. Heeren, M. Rumpf, M. Wardetzky, B. Wirth, Time-discrete geodesics in the space of shells. In Computer Graphics Forum, 2012.
• Y. Aflalo, A. Bronstein, M. Bronstein, R. Kimmel, Deformable Shape Retrieval by Learning Diffusion Kernels. In Scalespace, 2012.
• T. Windheuser, U. Schlickewei, Frank R. Schmidt, D. Cremers, Geometrically Consistent Elastic Matching of 3D Shapes: A Linear Programming Solution. In International Conference on Computer Vision (ICCV), 2011.
• R. Litman, A. Bronstein, Learning spectral descriptors for deformable shape correspondence. In PAMI, 2012.
• F. Mémoli, On the use of Gromov-Hausdorff distances for shape comparison. In Eurographics symposium on point-based graphics, 2007.
• J. Pokrass, A. M. Bronstein, M. M. Bronstein, P. Sprechmann, and G. Sapiro, Sparse modeling of intrinsic correspondences. In Computer Graphics Forum, 2013.
• M. Ovsjanikov, J. Sun, and L. Guibas, Global intrinsic symmetries of shapes. In Computer Graphics Forum, 2008.
• M. Ovsjanikov, Q. Mérigot, F. Mémoli and L. Guibas, One point isometric matching with the heat kernel. Computer Graphics Forum, 2010.